BLOQUE II APLICAS FUNCIONES ESPECIALES Y TRANSFORMACIONES DE GRAFICAS
2.1 FUNCION INVERSA
Dada una función  , se llama función inversa de
, se llama función inversa de  y se denota por
y se denota por  a otra función que para cualquier valor del dominio de
a otra función que para cualquier valor del dominio de  se cumple que:
se cumple que:
 , se llama función inversa de
, se llama función inversa de  y se denota por
y se denota por  a otra función que para cualquier valor del dominio de
a otra función que para cualquier valor del dominio de  se cumple que:
se cumple que:
No todas las funciones tienen inversa, para que exista se tiene que cumplir que para cada valor del recorrido de f  , proviene de un único valor del dominio
, proviene de un único valor del dominio  .
.
 , proviene de un único valor del dominio
, proviene de un único valor del dominio  .
.
Las gráficas de una función y su inversa son simétricas con respecto a la recta y=x
Para calcular la función inversa:
a) Se cambian los nombres de  e
e  .
.
 e
e  .
.
b) Se despeja la  .
.
 .
.
Calcula la inversa de la función  .
.
 .
.
Primero intercambiamos la  y la
y la  :
:  y después despejamos la
y después despejamos la  :
:
 y la
y la  :
:  y después despejamos la
y después despejamos la  :
:
Luego la función inversa de  es
es  .
.
 es
es  .
.
Vamos a comprobar que efectivamente es la inversa:


EJERCICIOS
Hallar la función inversa
1
2
3
4
5
6

7
8
9
10
1 Probar que: 

2Probar que: 

11
Probar que: 
Hallar la función inversa de:
12
13. Hallar la función inversa de:
14. Hallar la función inversa de:
15. Hallar la función inversa de:
16. Hallar la función inversa de:




17. Hallar la función inversa de:

18. Hallar la función inversa de:
19. Hallar la función inversa de:
20. Hallar la función inversa de:
2.2 FUNCION ESCALONADA
Una función escalonada es aquella función definida a trozos que en cualquier intervalo finito [a, b] en que esté definida tiene un número finito de discontinuidades c1 < c2 < ... < cn, y en cada intervalo ]ck, ck+1[ es constante, teniendo discontinuidades de salto en los puntos ck.
Informalmente, una función escalonada es aquella cuya gráfica tiene la forma de una escalera o una serie de escalones (que no necesariamente deben ser crecientes) al ser dibujada. El ejemplo más común de función escalonada es la función parte entera. Otras funciones escalonadas son la función unitaria de Heaviside o función escalón unitario, y la función signo.
Como caso general podemos ver la función y = s(x), definida así:![\begin{array}{rrcl}
s : & [-1,5 ] \in R & \to & R \\
& x & \to & y = s(x)
\end{array}](http://upload.wikimedia.org/math/a/e/7/ae7b5307d50533629a546e36fe7055fc.png)
![\begin{array}{rrcl}
s : & [-1,5 ] \in R & \to & R \\
& x & \to & y = s(x)
\end{array}](http://upload.wikimedia.org/math/a/e/7/ae7b5307d50533629a546e36fe7055fc.png)
En el intervalo cerrado [-1, 5] de números reales sobre los números reales, asociando a cada x de [-1,5] un valor de y, según el siguiente criterio:
Esta función tiene cuatro intervalos escalonados, como se ve en la figura.
La composición de cualquier función escalonada s(x) y una función cualquiera f(x) da por resultado una función escalonada g(x) = f(s(x)), siempre que f(x) esté definida para cualquier valor de x en el rango de s(x).
Evidentemente, la derivada de una función escalonada es 0 en cualquier punto en que se halle definida. No puede definirse en los puntos en que hay discontinuidades.
EJERCICIOS
ejem.
- Analizar situaciones que se pueden modelar utilizando la función escalonada
Veamos algunos ejemplos:
1. Felipe necesita ANILLAR un informe para llevar a su Liceo. YOBILO
Entra en una librería que muestra la siguiente lista:
ANILLADOS
| |
1 – 50
|
$ 420
|
51 - 100
|
$ 800
|
101 - 150
|
$ 920
|
151 - 200
|
$ 1300
|
Construye el grafico según los datos de la tabla, y responde:
1 ¿Cuánto deberá pagar por el anillado de un informe que tiene 27 páginas?
2.- ¿Cuánto deberá pagar por el anillado de un informe que tiene 80 páginas?
3.- ¿Cuánto dinero pagará en total por los dos anillados?
4.- Si anillara los dos informes juntos, ¿Cuánto pagaría?
6 .- ¿Qué puedes decir del gráfico ?
2.- Los alumnos del 2º año A del Liceo YOBILO necesitan reunir dinero para fin de año para conseguir su objetivo deciden vender Helados Natalie va a una fábrica de helados, donde encuentra la siguiente lista:
HELADOS CHOCO - PANDA
| |
Cantidad
|
Precio unitario
|
0 – 50
|
$ 80
|
51 - 100
|
$ 70
|
101 -150
|
$ 60
|
151 - 200
|
$50
|
HELADOS DE AGUA
| |
Cantidad
|
Precio unitario
|
1 – 25
|
$ 60
|
26 - 50
|
$ 50
|
51 -100
|
$ 45
|
101 - 150
|
$35
|
Haz el gráfico para cada situación y luego calcula:
Cuánto se debe pagar por: a) 100 choco pandas y 150 de frutas
b) 40 de frutas y 130 choco pandas
c) Es conveniente comprar al por mayor o al detalle?
d) Qué conclusión sacas de esta situación?
3.) Una Empresa vende artículos para cumpleaños y presenta las siguientes listas De precio
GLOBOS
| |
Cantidad
|
Precio unitario
|
1– 100
|
$ 100
|
101 - 300
|
$ 90
|
301 - 500
|
$ 80
|
501- 1000
|
$ 50
|
GORROS
| |
Cantidad
|
Precio unitario
|
1 – 25
|
$ 250
|
26 - 50
|
$ 220
|
51 -100
|
$ 190
|
Mas de100
|
$150
|
SERPENTINAS
| |
Cantidad
|
Precio unitario
|
1 – 50
|
$ 30
|
51- 100
|
$ 27
|
101 – 150
|
$ 24
|
151 - 200
|
$20
|
Haz el gráfico para cada situación y luego calcula ¿Cuánto debes pagar por:
a) 200 globos, 24 gorros y 120 serpentinas
b) 100 globos, 30 gorros y 100 serpentinas
c) 310 globos, 50 gorros y 180 serpentinas
III) Abre el texto en la página 65 y desarrolla el ejercicio Nº 3 junto a tu compañera
Francisca está buscando trabajo .En un restaurante le ofrecen trabajar como garzona los fines de semana. Le dicen “Tu sueldo dependerá de lo que vendas diariamente, aquí se ve claramente”, y le muestran el gráfico
a) Pero francisca no entiende el gráfico.¿Cómo le explicas a ella lo que ganara en ese trabajo?
b) ¿Qué error tiene el gráfico presentado?
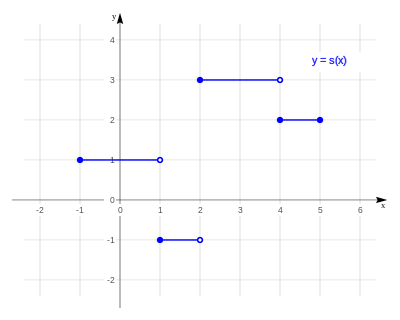
2.3 FUNCION VALOR ABSOLUTO
Recordemos que la definición del valor absoluto surge de nociones geométricas, y se relaciona con los conceptos de longitud y distancia.
La función de valor absoluto tiene por ecuación f(x) = |x|, y siempre representa distancias; por lo tanto, siempre será positiva o nula.
En esta condición, de ser siempre positiva o nula, su gráfica no se encontrará jamás debajo del eje x. Su gráfica va a estar siempre por encima de dicho eje o, a lo sumo, tocándolo.
Las funciones en valor absoluto siempre representan una distancia o intervalos (tramos o trozos) y se pueden resolver o calcular siguiendo los siguientes pasos:
1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces (los valores de x).
2. Se forman intervalos con las raíces (los valores de x) y se evalúa el signo de cada intervalo.
3. Definimos la función a intervalos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función.
4. Representamos la función resultante.
EJEMPLOS:
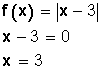
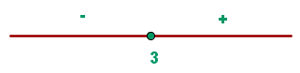
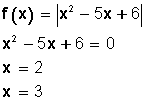
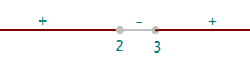

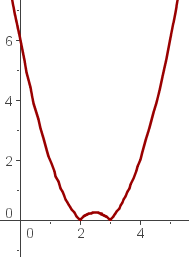
Representa las función valor absoluto:
f(x) = |x - 2|


Representa las función valor absoluto e indica su dominio.



D= 

Representa las función valor absoluto e indica su dominio:





D=

Representa las función valor absoluto:
f(x) = |x² -4x + 3|
x² -4x + 3 = 0 x = 1 x = 3



Representa las función valor absoluto:
f(x) = |-x² + 5x - 4|
-x² + 5x - 4 =0 x² - 5x + 4 =0 x = 1 x = 4



Representa las función valor absoluto:
f(x) = |x| − x
x = 0


 Representa las función valor absoluto:
Representa las función valor absoluto:
f(x) = |x| / x
x = 0



2.4 FUNCION IDENTIDAD
En matemáticas una función identidad es una función matemática, de un conjunto M a sí mismo, que devuelve su propio argumento.
a función identidad puede describirse de la forma siguiente:
o tambien:
La función identidad es trivialmente idempotente, es decir:

Ejemplos
La función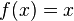 de
de  en
en  tiene como representación gráfica en el eje de coordenadas la línea recta que cruza el origen subiendo en un ángulo de 45° hacia la derecha.La función identidad en
tiene como representación gráfica en el eje de coordenadas la línea recta que cruza el origen subiendo en un ángulo de 45° hacia la derecha.La función identidad en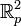 (el plano de los reales tomando las coordenadas polares) es la función determinada por la ecuación
(el plano de los reales tomando las coordenadas polares) es la función determinada por la ecuación  : una espiral que se aleja del origen uniformemente en el sentido contrario a las agujas del reloj.La función identidad en
: una espiral que se aleja del origen uniformemente en el sentido contrario a las agujas del reloj.La función identidad en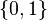 es la doble negación, expresada por
es la doble negación, expresada por 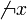 .
.
FUNCIÓN IDENTIDAD
Su funcion Basica es F(x)=X Su nombre probiene del hecho, que el valor del dominio (X),sera el mismo o identico valor que el contradominio (Y)con esta condiccion es una funcion unica.
- *Funcion Continua
- *Dominio del (-) infinito hasta mas infinito.
- *Es de primer grado ( Linea Recta )
- *Tiene pendiente, 1 creciente
- *Su alguno de inclinacion es de 45 grados
- *Debe pasar por el origen
- *A la vez es biyectiva, Inyectiva
La función identidad es del tipo:
f(x) = x
Su gráfica es la bisectriz del primer y tercer cuadrante.
Por tanto la recta forma con la parte positiva del eje de abscisas un ángulo de 45º y tiene de pendiente: m = 1.

2.5 FUNCION CONSTANTE
La función constante es
aquella en la que para cualquier valor de la variable independiente ( x
), la variable dependiente ( f(x)
) no cambia, es decir, permanece constante.
Sea f(x)=c. El dominio de esta función es el conjunto de todos los
reales, y el contradominio es únicamente el real c.
Ejemplo 1.
La función f(x)
= 4 es una función constante porque
independientemente del valor de x el valor de la función siempre es 4.
Otra manera de representar una función es por medio de una
lista de parejas ordenadas de la forma (
x, f(x)) frecuentemente en una tabla.
Ejemplo 2.
La función f(x)=3
se
puede representar en forma tabular para algunos valores de x:
x
|
f(x)
|
-1
|
3
|
0
|
3
|
1
|
3
|
raiz cuadrada de 2
|
3
|
1.5
|
3
|
5/2
|
3
|
La gráfica de esta función para los valores de x
entre -3 y 3
es:
Ejemplo 3.
Sea la función f(x)=-2 , encontrar su representación tabular y gráfica.
|
||||||||||||||
Una función constante
f(x) = c :
- tiene
el mismo valor de y = f(x) para cualquier valor
de x,
- tiene
como gráfica una línea horizontal,
- nunca
cruza el eje x, excepto cuando
f(x) = 0,
- cruza
una sola vez el eje y en el punto (0, c),
- es
aquella en que el exponente máximo de la x es cero,
Función constante ⇒ y = n
La fórmula de la función constante es: y = n
La pendiente de la recta m = 0, no es ni creciente ni decreciente
No hace falta hacer tabla de valores la recta vale siempre n
Estudiar y representar la siguiente recta y = 3
La pendiente de la recta es 0, n = 3
Gráfica

_____________________________________________________________________________________________



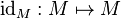



.gif)
No hay comentarios:
Publicar un comentario