BLOQUE I. RECONOCES Y REALIZAS OPERACIONES CON DISTINTOS TIPOS DE FUNCIONES
- FUNCIONES
Una función es cuando dos variables están relacionadas de tal manera que el valor de la primera queda determinado si se da un valor a la segunda, entonces se dice que la primera es función de la segunda
En matemáticas una función es inyectiva si a cada conjunto del dominio le corresponde un valor distinto que el del conjunto imagen. es decir a cada elemento del conjunto Y le corresponde un solo valor de X tanto que en el conjunto X no puede haber dos o mas elementos con la misma imagen.
-FUNCIONES SOBREYECTIVAS
También se le llama suryectiva y es aquella función en que todos los valores de Y (el co-dominio) son imagen de un valor de X (el dominio).
-FUNCIONES BIYECTIVAS
En matemáticas, una función es biyectiva si es al mismo tiempo inyectiva y sobreyectiva; es decir, si todos los elementos del conjunto de salida tienen una imagen distinta en el conjunto de llegada, y a cada elemento del conjunto de llegada le corresponde un elemento del conjunto de salida.
Formalmente, dada una función  :
:
 :
:
La función es biyectiva si se cumple la siguiente condición:
Es decir, si para todo  de
de  se cumple que existe un único
se cumple que existe un único  de
de  , tal que la función evaluada en
, tal que la función evaluada en  es igual a
es igual a  .
.
 de
de  se cumple que existe un único
se cumple que existe un único  de
de  , tal que la función evaluada en
, tal que la función evaluada en  es igual a
es igual a  .
.
Dados dos conjuntos  e
e  finitos, entonces existirá una biyección entre ambos si y sólo si
finitos, entonces existirá una biyección entre ambos si y sólo si  e
e  tienen el mismo número de elementos.
tienen el mismo número de elementos.
 e
e  finitos, entonces existirá una biyección entre ambos si y sólo si
finitos, entonces existirá una biyección entre ambos si y sólo si  e
e  tienen el mismo número de elementos.
tienen el mismo número de elementos.
-FUNCIONES INVERSAS
La función inversa es para saber cual es la función de modo que valla de B hacia A, es por eso que se despeja X para observar como seria la función en "sentido contrario" y después se intercambia X por Y porque X que era el dominio de la función inversa pasa de ser el dominio de la función inversa.
1.2 RELACIONES
1.4 CONTRADOMINIO E IMAGEN
1.2 RELACIONES
Es la correspondencia de un primer conjunto llamado dominio, con un segundo conjunto, llamado rango, a manera que cada elemento del dominio le corresponde uno o mas elementos del recorrido o rango. por su parte, una función es una relación en la cual se añade la condición de que a cada valor del dominio le corresponde uno y solo un valor del recorrido.
1.3 DOMINIO
Es la funcion, es el conunto de numeros reales X para que los que la expresion (F)(X) tiene sentido y produce un numero real y por ejemplo, el dominio de la funcion h(x)=1/x es el conjunto de todos los numeros reales diferentes a cero, porque 1/x esta definida presisamente cuando X es mayor o menor que 0.
1.4 CONTRADOMINIO E IMAGEN
En matemáticas, la imagen (conocida también como campo de valores o rango) de una función  es el conjunto formado por todos los valores que puede llegar a tomar la función. Se puede denotar como
es el conjunto formado por todos los valores que puede llegar a tomar la función. Se puede denotar como 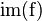 ,
,  o bien
o bien  y formalmente está definida por:
y formalmente está definida por:
 es el conjunto formado por todos los valores que puede llegar a tomar la función. Se puede denotar como
es el conjunto formado por todos los valores que puede llegar a tomar la función. Se puede denotar como 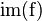 ,
,  o bien
o bien  y formalmente está definida por:
y formalmente está definida por:
Adicionalmente, es posible hablar de la imagen de un elemento (del dominio) para hacer referencia al valor que le corresponde bajo la función. Esto es, si  es una función, entonces la imagen del elemento
es una función, entonces la imagen del elemento 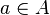 es el elemento
es el elemento  .
.
 es una función, entonces la imagen del elemento
es una función, entonces la imagen del elemento 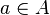 es el elemento
es el elemento  .
.
Es importante diferenciar el concepto de contradominio del concepto de conjunto imagen.
Si  es una función, al conjunto Y de valores que podría tomar la función se conoce como contradominio, mientras que el conjunto imagen consta únicamente de los valores que realmente toma.
es una función, al conjunto Y de valores que podría tomar la función se conoce como contradominio, mientras que el conjunto imagen consta únicamente de los valores que realmente toma.
 es una función, al conjunto Y de valores que podría tomar la función se conoce como contradominio, mientras que el conjunto imagen consta únicamente de los valores que realmente toma.
es una función, al conjunto Y de valores que podría tomar la función se conoce como contradominio, mientras que el conjunto imagen consta únicamente de los valores que realmente toma.
Por ejemplo, la función  tiene por contradominio el conjunto de todos los números reales, pero como nunca toma realmente valores negativos, el conjunto imagen está formado únicamente por los números reales no negativos.
tiene por contradominio el conjunto de todos los números reales, pero como nunca toma realmente valores negativos, el conjunto imagen está formado únicamente por los números reales no negativos.
 tiene por contradominio el conjunto de todos los números reales, pero como nunca toma realmente valores negativos, el conjunto imagen está formado únicamente por los números reales no negativos.
tiene por contradominio el conjunto de todos los números reales, pero como nunca toma realmente valores negativos, el conjunto imagen está formado únicamente por los números reales no negativos.
En general, el conjunto imagen siempre es un subconjunto del codominio, y cuando éstos coinciden, se dice que la función es suprayectiva.
1.5 REGLA DE CORRESPONDENCIA
Una correspondencia unívoca es una correspondencia matemática donde cada elemento del conjunto dominio se corresponde con solo un elemento del conjunto rango.
Una correspondencia biunívoca es simplemente una correspondencia univoca cuya correspondencia inversa también es unívoca. Es decir: cada elemento del primer conjunto se corresponde con solo un elemento del segundo conjunto, y cada elemento del segundo conjunto se corresponde con solo un elemento del primer conjunto.


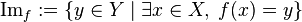

.png)
No hay comentarios:
Publicar un comentario