BLOQUE IV  UTILIZAS FUNCIONES POLINOMIALES DE GRADOS TRES Y  CUATRO

4.1 MODELO MATEMÁTICO DE LAS FUNCIONES POLINOMIALES DE GRADOS: TRES Y CUATRO

FUNCIÓN POLINÓMICA DE GRADO 3

Se denomina función cúbica a toda función de la forma:

y= ax³ + bx² + cx+ d; donde a (distinto de 0), b, c y d son números reales.

                

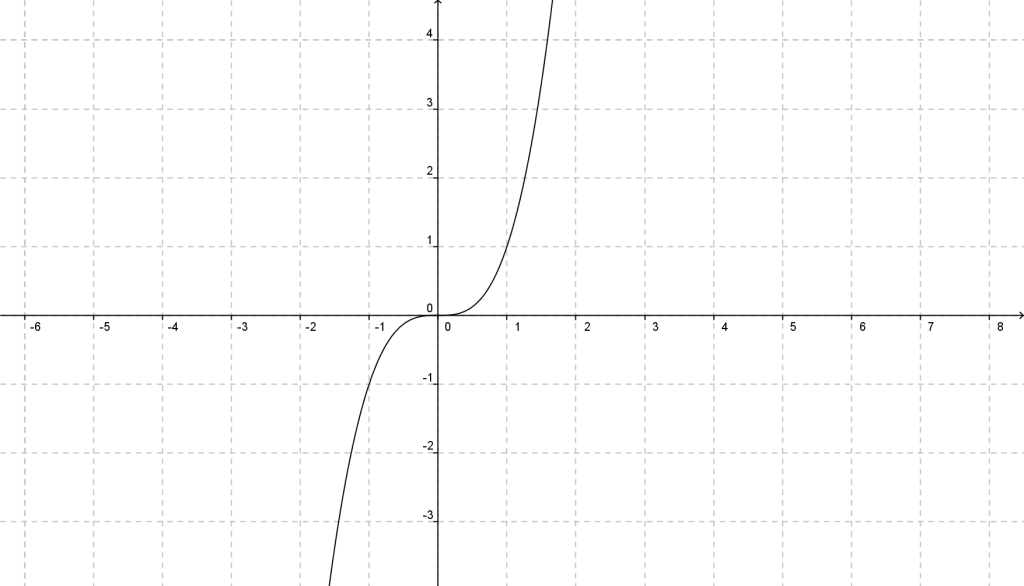
Función polinomial de tercer grado

La función polinomial de tercer grado es toda aquella función que se puede escribir de la forma:

y = a3x3 + a2x2 + a1x + a0

donde a3 = 0.

La función polinomial de tercer grado también se conoce como función cúbica

La función polinomial de tercer grado más sencilla es:

y = x3

Grafícala, encuentra sus raíces, dominio y contradominio.

-Empezamos calculando sus raíces

- Para que y = 0 se requiere que x3 = 0.

-En palabras esto nos está diciendo que debemos encontrar los números que al multiplicarlos

por sí mismo tres veces obtengamos cero

- El único número que satisface la condición anterior es x = 0

-Esta es la única raíz de la función.

-Para encontrar el dominio recuerda que el dominio de cualquier función polinomial es el

conjunto de los números reales.

-El contradominio se calcula de la sigiuente manera:

* Observa que cuando x es positivo, el resultado de elevarlo al cubo es positivo también.

* Cuando x es negativo el resultado de elevarlo alcubo es negativo

-Entonces, el contradominio también es el conjunto de los números reales, porque cuando x

crece mucho los resultados de elevarlo al cubo también crece mucho.

-Esto mismo pasa con valores tanto positivos como negativos.

FUNCIÓN POLINÓMICA DE GRADO 4

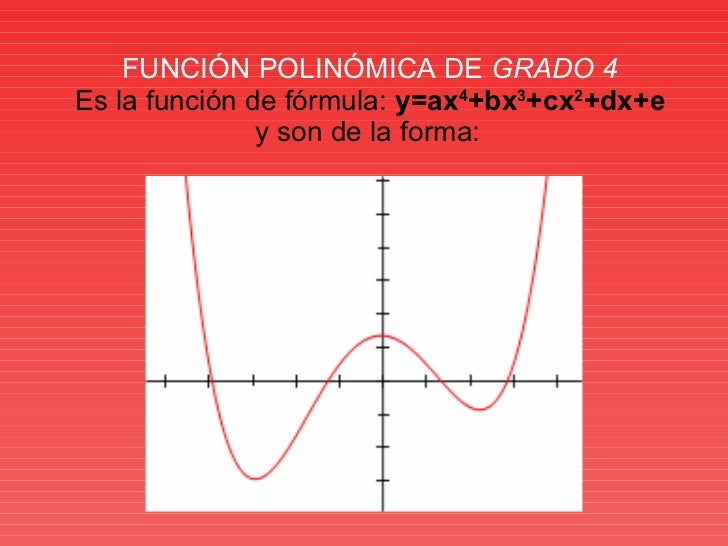Es la función de fórmula: y = ax⁴+ bx³+ cx²+ dx+ e; donde a (distinto de 0), b, c, d y e son números reales.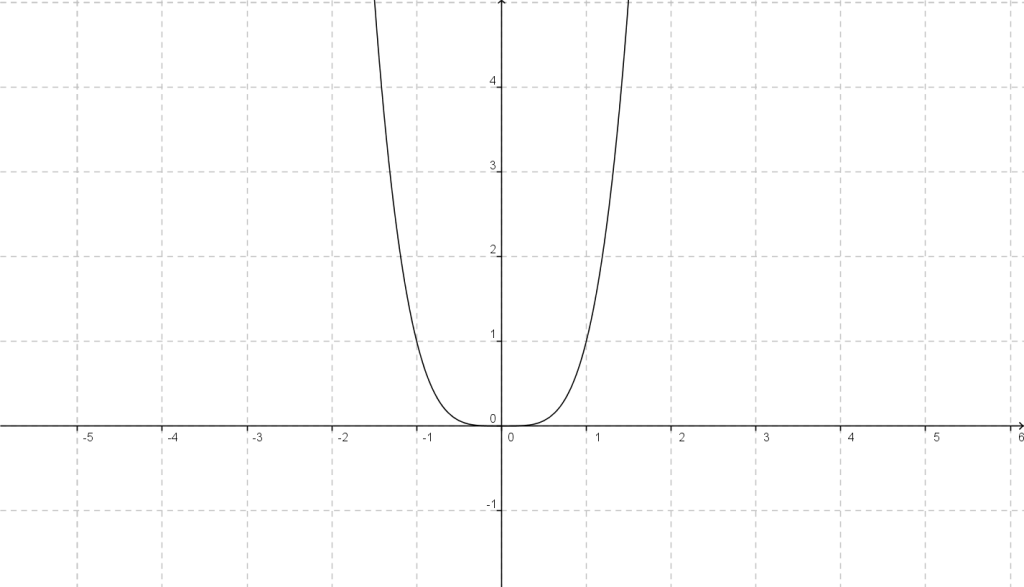

Una representación especial de las funciones polinomiales es la función que no tiene un exponente como los anteriores.

4.2 PROPIEDADES GEOMETRICAS DE LAS FUNCIONES POLINOMIALES DE GRADOS: TRES Y CUATRO

Propiedades Algebraicas y Geométricas de las Funciones Cuadráticas de Segundo Grado ó Parabólicas
Se llama función cuadrática a aquella cuya expresión algebraica en una sola variable es de gado dos. Y se les dice parabólicas o de parábola, porque su gráfica es una parábola.

Donde:
y es la variable dependiente
x la variable independiente
a.x2 es el término cuadrático
a es el coeficiente cuadrático
b.x es el término lineal
b es el coeficiente lineal
c es el término independiente

Dado que el cuadrado de números opuestos es siempre positivo, la gráfica de esta función es una parábola, cuyas ramas estarán para el lado positivo del eje de las ordenadas si a es positivo, caso contrario si a es negativo.-
O sea que:
Función positiva: las ramas de la parábola hacia la parte positiva del eje de las ordenadas (arriba)
Función negativa: las ramas de la parábola hacia la parte negativa del eje de las ordenadas (abajo)

4.3  MÉTODOS DE SOLUCIÓN DE LAS ECUACIONES FACTORIZABLES ASOCIADAS A UNA FUNCIÓN POLINOMIAL DE GRADOS: TRES Y CUATRO.

Métodos de solución de ecuaciones factorizables a una función polinomial 

Para identificar las aplicaciones una función polinomial de grado tres, presentamos una situación común de construcción.

Se tiene una hoja cuadrada de cartón de72 cm de lado y quieres construir una caja para sus cosas recortando un cuadrado de cada esquina. ¿Cuáles deben ser las dimensiones del cuadrado recortado para que el volumen de la caja sea el máximo?

En esta situación se dispone de la lámina completa en la que se puede recortar un cuadrado de lado “x”. al cortar cada esquina y doblar las partes restantes para obtener la caja de base cuadrada cuyas dimensiones son, en la base, 72 – 2x centímetros de lado y una altura             de x centímetros.

El volumen de cualquier caja se obtiene como el producto de cada una de sus aristas, para este caso:

V= (72-2x)² x y desarrollando y simplificando se obtiene:

V = 4x³ – 288x² + 5 184x

Esta expresión algebraica determina el volumen máximo, pero necesitamos saber cuánto hay que recortar para que así sea. Pero si encontramos las raíces de esta función obtenernos el valor para que sea cero la función y no el valor de x para un mayor volumen. Al realizar un tabla de valores para x y y, encontraremos que hay un máximo volumen en 12 centímetros

nción f(x)=x

+3x

2

-4x-12=0


F(-2)=0

4.4 REPRESENTACIÓN GRÁFICA DE FUNCIONES POLINOMIALES DE GRADOS: TRES Y CUATRO

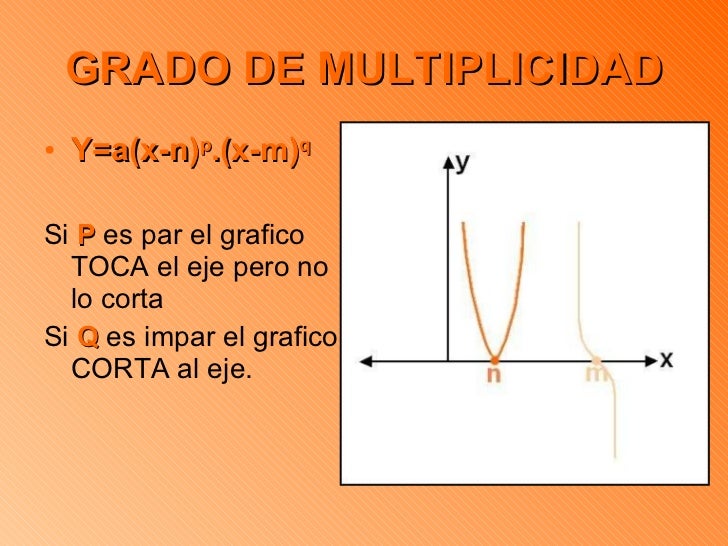
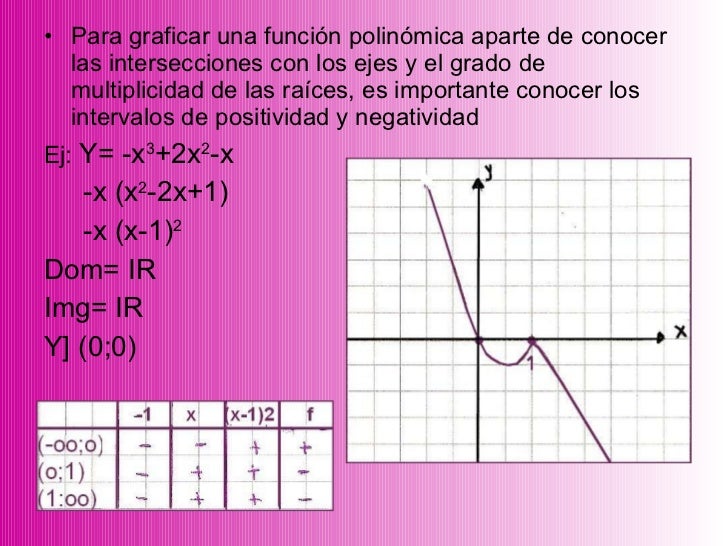
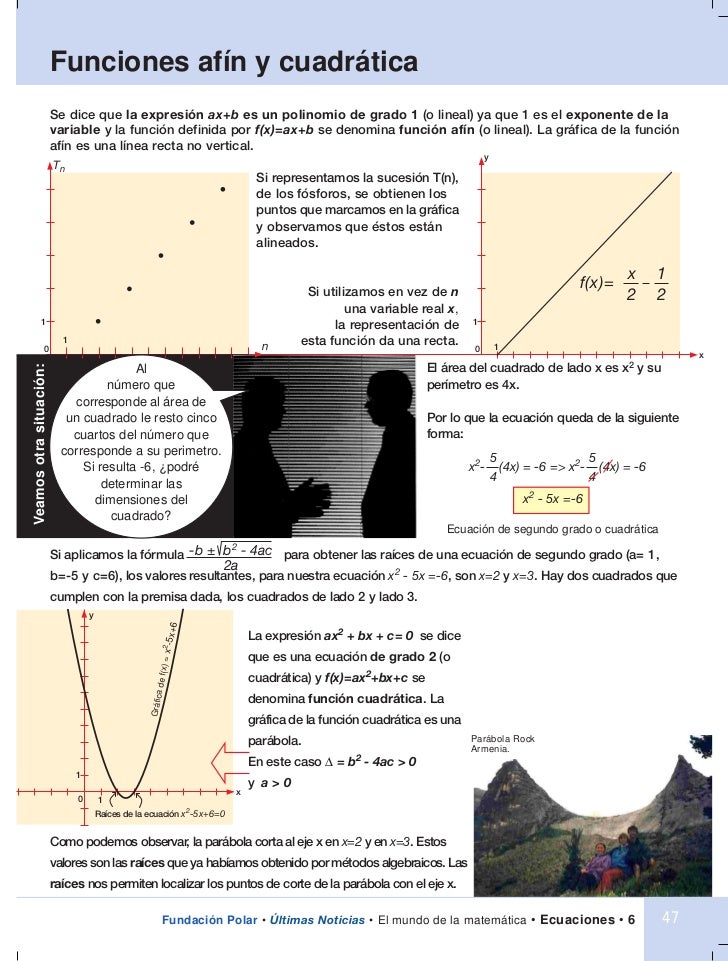
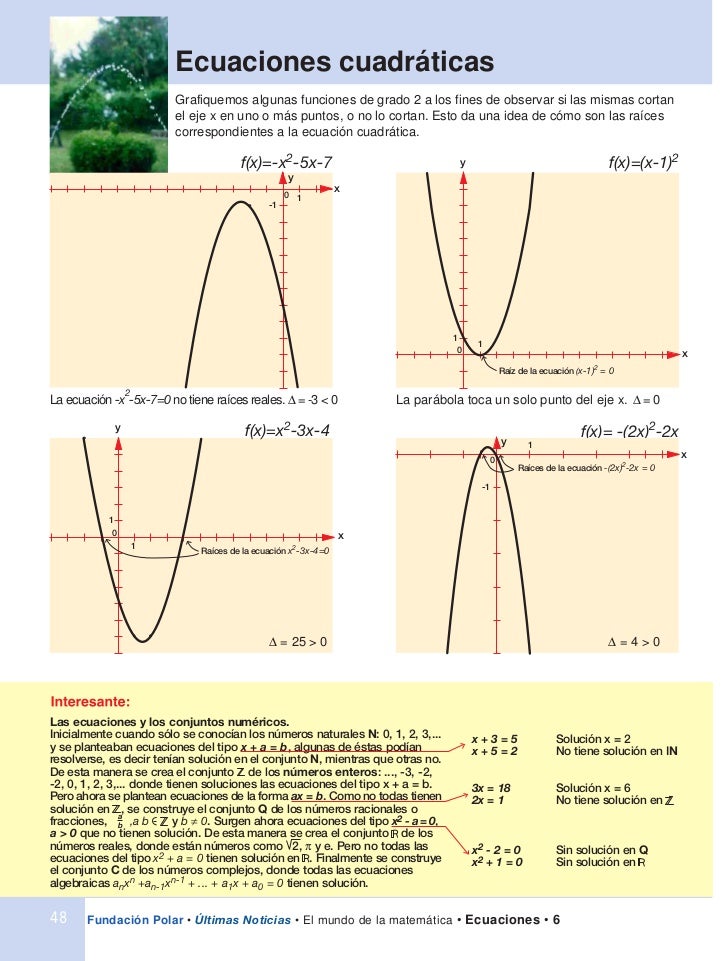
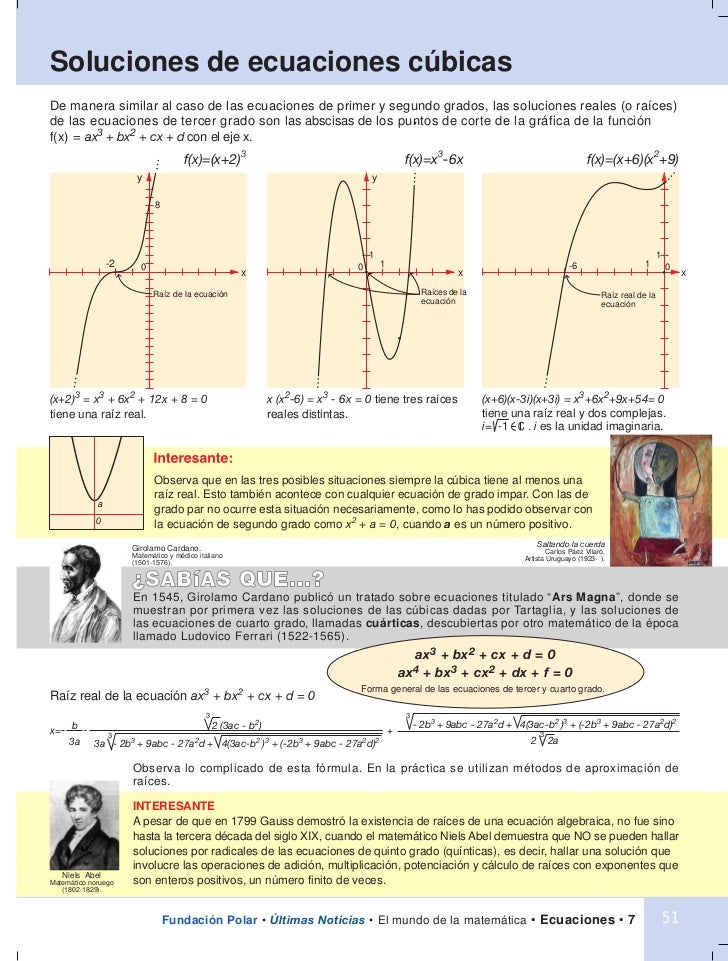
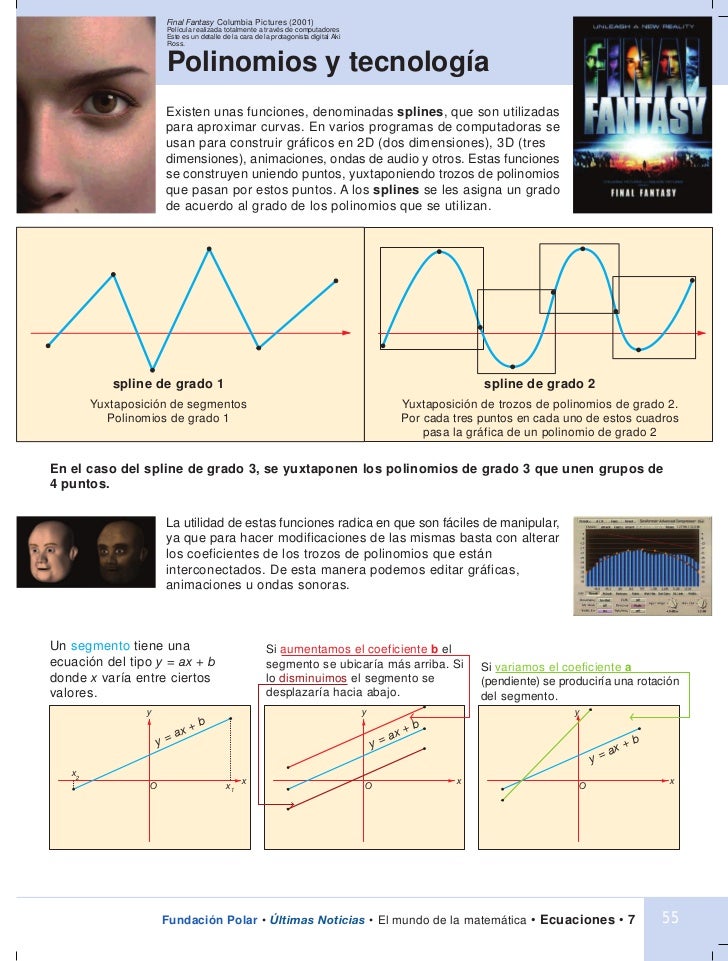
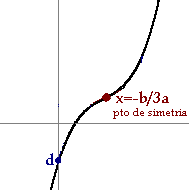
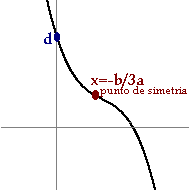
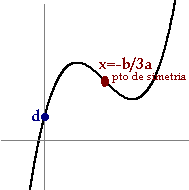
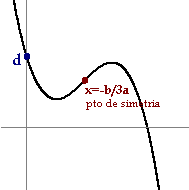
• Las cúbicas: f(x)=ax³+bx²+cx+d son como sillas, unas con el asiento hundido y otras sin hundir, podemos observar que el signo de a decide si el respaldo de la silla está a la derecha o a la izquierda y todas son simétricas respecto del punto en el que la x vale -b/3a, punto de inflexión. 

En este caso, no basta con el coeficiente a del máximo grado para saber la forma de la función, tal y como ocurre con las gráficas de las funciones polinómicas de menor grado (Ir al cuadro)

                       

.
.		f(x)=ax3+bx2+cx+d					.
.	a+					a-		.
.								.
.					.