BLOQUE V UTILIZAS FUNCIONES FACTORIZABLES EN LA RESOLUCIÓN DE PROBLEMAS
5.1 CEROS Y RAICES DE LA FUNCION
CEROS Y RAÍCES
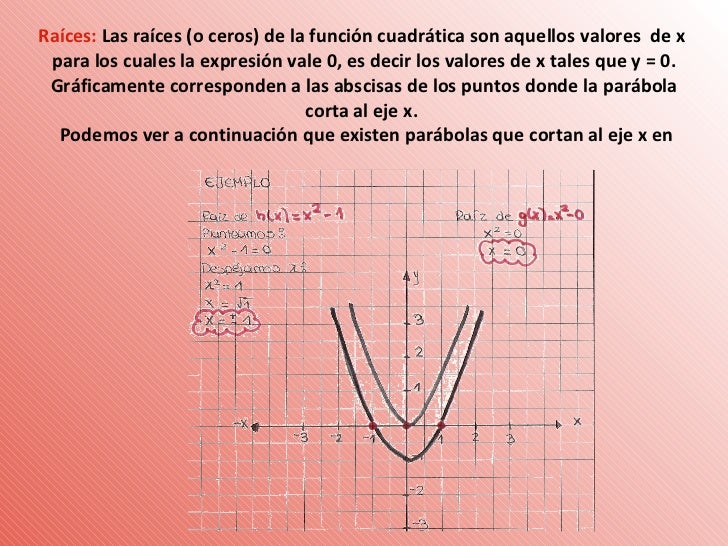
Con lo cual se comprueba que −4, −1, 2 y 3 sí son raíces del polinomio. Además, si graficamos la función polinomial se observa que el polinomio intersecta al eje x en los valores de las raíces.
TEOREMA DEL FACTOR
En álgebra, el teorema del factor sirve para encontrar los factores de un polinomio (una expresión en la cual los términos sólo son sumados, sustraídos o multiplicados, e.g.  ). Es un caso especial del teorema del resto.
). Es un caso especial del teorema del resto.
 ). Es un caso especial del teorema del resto.
). Es un caso especial del teorema del resto.
El teorema del factor establece que un polinomio 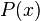 tiene un factor
tiene un factor  si y sólo si
si y sólo si  es una raíz de
es una raíz de 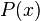 , es decir que
, es decir que  .
.
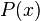 tiene un factor
tiene un factor  si y sólo si
si y sólo si  es una raíz de
es una raíz de 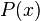 , es decir que
, es decir que  .
.
TEOREMA DEL RESIDUO
- Teorema que establece que si un polinomio de x, f(x), se divide entre (x - a), donde a es cualquier número real o complejo, entonces el residuo es f(a).Por ejemplo, si f(x) = x2 + x - 2 se divide entre (x-2), el residuo es f(2) = 22 + (2) - 2 = 4. Este resultado puede volverse obvio si cambiamos el polinomio a una de las siguientes formas equivalentes:f(x) = (x-2)(x+3) + 4Como se muestra, la expresión anterior nos puede llevar fácilmente a esperar que 4 sea el residuo cuando f(x) se divide entre (x-2).El teorema del residuo nos puede ayudar a encontrar los factores de un polinomio. En este ejemplo, f(1) = 12 + (1) - 2 = 0. Por lo tanto, significa que no existe residuo, es decir, (x-1) es un factor. Esto puede mostrarse fácilmente una vez que reacomodamos el polinomio original en una de las siguientes expresiones equivalentes:f(x) = (x-1)(x+2)Como se muestra, (x-1) es un factor.
Teoremas del residuo y del factor.
Algoritmo de la división.
Para cada polinomio  de grado mayor o igual a uno y para cada número
de grado mayor o igual a uno y para cada número  , existe un polinomio único
, existe un polinomio único  de un grado menor que el de
de un grado menor que el de  y un número único R, tal que:
y un número único R, tal que:
Al polinomio  se le denomina cociente,
se le denomina cociente,  en el divisor y R es el residuo.
en el divisor y R es el residuo.
Teorema del residuo. Si  es el residuo de dividir el polinomio
es el residuo de dividir el polinomio  entre
entre  , entonces
, entonces  .
.
Demostración.
Como  por el algoritmo de la división, se tiene que si
por el algoritmo de la división, se tiene que si  ,
,  .
.
O sea,  .
.
Ejemplo 7.
Hállese el residuo de dividir el polinomio  entre
entre  .
.
Solución.
O sea que el residuo es 2.
Teorema del factor. Si  es un cero del polinomio
es un cero del polinomio  , entonces
, entonces  es un factor de
es un factor de  .
.
Demostración.
Si  es un cero de
es un cero de  ,
,  .
.
Pero por el algoritmo de la división  .
.
Como  ,
,  .
.
Por tanto,  y
y  .
.
Ejemplo 8.
Use el teorema del factor para probar que  es un factor de
es un factor de  .
.
Solución.
Luego –1 es un cero de  .
.
Así  es un factor de
es un factor de  .
.
ejemplo.
Si se desea encontrar los factores de  , para ello se podría tantear un primer factor,
, para ello se podría tantear un primer factor, 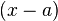 . Si el resultado de sustituir
. Si el resultado de sustituir  en el polinomio es igual a 0, se sabe que hay un factor. ¿Es
en el polinomio es igual a 0, se sabe que hay un factor. ¿Es  un factor? Para saberlo, se sustituye
un factor? Para saberlo, se sustituye 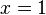 en el polinomio:
en el polinomio:
 , para ello se podría tantear un primer factor,
, para ello se podría tantear un primer factor, 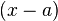 . Si el resultado de sustituir
. Si el resultado de sustituir  en el polinomio es igual a 0, se sabe que hay un factor. ¿Es
en el polinomio es igual a 0, se sabe que hay un factor. ¿Es  un factor? Para saberlo, se sustituye
un factor? Para saberlo, se sustituye 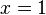 en el polinomio:
en el polinomio:
Cómo esta operación da 18 (y no 0),  no es un factor de
no es un factor de  . Así que ahora se prueba con
. Así que ahora se prueba con  (sustituyendo
(sustituyendo 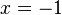 en el polinomio):
en el polinomio):
 no es un factor de
no es un factor de  . Así que ahora se prueba con
. Así que ahora se prueba con  (sustituyendo
(sustituyendo 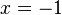 en el polinomio):
en el polinomio): .
.
Que da como resultado 0. Por tanto,  , que es equivalente a
, que es equivalente a 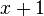 , es un factor, y -1 es una raíz de
, es un factor, y -1 es una raíz de  .
.
 , que es equivalente a
, que es equivalente a 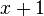 , es un factor, y -1 es una raíz de
, es un factor, y -1 es una raíz de  .
.
Las otras dos raíces se pueden encontrar dividiendo  entre
entre  para obtener un polinomio de segundo grado, que se puede resolver de la siguiente manera
para obtener un polinomio de segundo grado, que se puede resolver de la siguiente manera 
 entre
entre  para obtener un polinomio de segundo grado, que se puede resolver de la siguiente manera
para obtener un polinomio de segundo grado, que se puede resolver de la siguiente manera 
Ejercicio
Comprueba que los siguientes polinomios tienen como factores los que se indican:
1(x3 − 5x − 1) tiene por factor (x − 3)
(x3 − 5x −1) es divisible por (x − 3) si y sólo si P(x = 3) = 0.
P(3) = 33 − 5 · 3 − 1 = 27 − 15 − 1 ≠ 0
(x − 3) no es un factor.
2(x6 − 1) tiene por factor (x + 1)
(x6 − 1) es divisible por (x + 1) si y sólo si P(x = − 1) = 0.
P(−1) = (−1)6 − 1 = 0
(x + 1) es un factor.
3(x4 − 2x3 + x2 + x − 1) tiene por factor (x − 1)
(x4 − 2x3 + x2 + x − 1) es divisible por (x − 1 ) si y sólo si P(x = 1) = 0.
P(1) = 14 − 2 · 13 + 1 2 + 1 − 1 = 1 − 2 + 1 + 1 − 1 = 0
(x − 1) es un factor.
4(x10 − 1024) tiene por factor (x + 2)
(x10 − 1024) es divisible por (x + 2) si y sólo si P(x = − 2) = 0.
P(−2) = (−2)10 − 1024 = 1024 − 1024 = 0
(x + 2) es un factor.
Calculo las raíces del polinomio:
Q(x) = x2 − x − 6
Los divisores del término independiente son ±1, ±2, ±3.
Q(1) = 12 − 1 − 6 ≠ 0
Q(−1) = (−1)2 − (−1) − 6 ≠ 0
Q(2) = 22 − 2 − 6 ≠ 0
Q(−2) = (−2)2 − (−2) − 6 = 4 +2 +6 = 0
Q(3) = 32 − 3 − 6 = 9 − 3 − 6 = 0
x = −2 y x = 3 son las raíces o ceros del polinomio: P(x) = x2 − x − 6, porque P(−2) = 0 y P(3) = 0.
P(x) = (x + 2) · (x − 3)
La división sintética se realiza para simplificar la división de un polinomio entre otro polinomio de la forma x – c, logrando una manera mas compacta y sencilla de realizar la división.
Ilustraremos como el proceso de creación de la división sintética con un ejemplo:
Comenzamos dividiéndolo normalmente
Pero resulta mucho escribir pues repetimos muchos términos durante el procedimiento, los términos restados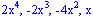 pueden quitarse sin crear ninguna confusión, al igual que no es necesario bajar los términos
pueden quitarse sin crear ninguna confusión, al igual que no es necesario bajar los términos 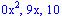 . al eliminar estos términos repetidos el ejercicio nos queda:
. al eliminar estos términos repetidos el ejercicio nos queda:
Ahora si mantenemos las potencias iguales de x en las columnas de cada potencia y colocando 0 en las faltantes se puede eliminar el escribir las potencias de x, así:
El Teorema Fundamental del Algebra (TFA) dice que todo polinomio a coeficientes complejos tiene un raíz compleja, es decir existe un número complejo donde el polinomio evalua a cero. Hay muchas demostraciones de este importante resultado. Todas requieren bastantes conocimientos matemáticos para formalizarlas. Sin embargo, si se deja de lado algo del rigor matemático, hay argumentos simples y creibles, que le permiten a uno convencerse de la veracidad del TFA. Nuestro objetivo es presentar a continuación uno de estos argumentos.
Consideremos entonces un polinomio P(z) cualquiera de grado n. Luego, su n-ésimo coeficiente Pn no puede ser igual a 0. SiP(0)=0, estarímos listos pues tendríamos que 0 es una raíz de P. Supondremos entonces que se tiene el caso no trivial, es decir, queP(0) no es 0. Notar que esto significa que P0 es distinto de 0, puesto que P(0)=P0.
Sea Cr al conjunto de números complejos de módulo r, i.e., Cr= { z : |z|=r }. Geométricamente dichos números están ubicados en un círculo de radio r en torno al origen del plano complejo. Por ejemplo, si r=1, entonces Cr es:

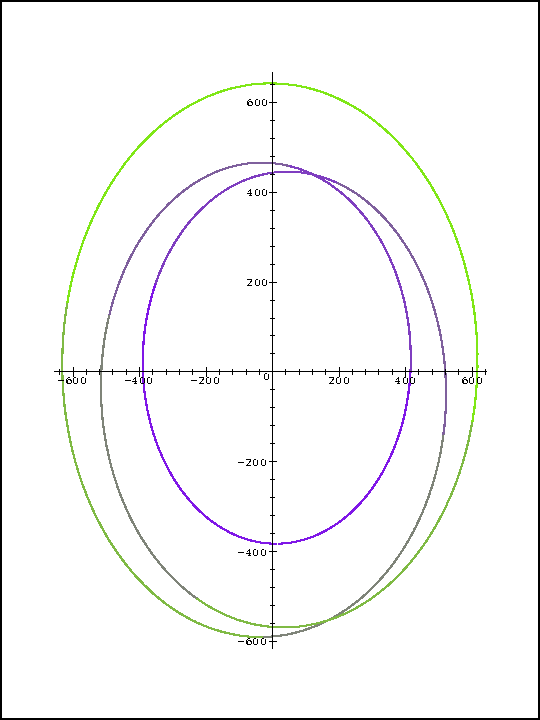
Sea además P(Cr) la imágen a través de P de Cr, i.e., P(Cr)={ P(z) : |z|=r }. Observar que P(Cr) es una curva cerrada. ¿Porqué? Observar también que si r es suficientemente pequeño (cuán pequeño dependerá de los valores de los coeficientes del polinomioP), entonces todo elemento de P(Cr) estará muy cerca de P0 en el plano complejo y el origen del plano complejo estará en el"exterior" de la curva P(Cr). ¿Porqué? Por ejemplo, si P(z)=(2+2I)-1.5*·z+2I·z2+I·z3 y r=0.75, entonces P(Cr) es:



No hay comentarios:
Publicar un comentario